context
In 2021 March, i had to write a paper called the “Extended Essay”, which was sort of the culminating work for the International Baccalaureate program at my high school. I was one of the 3.2% of candidates to write it under the “Mathematics” subject and one of 20% to earn an A for it!1 :D
Even though it’s poorly written, i decided to throw it up here, with some of the cruft trimmed off. The conclusion is that tangent lines to circles can be modeled by the following system of equations.
$$ \begin{aligned} a &= x_1-x_2 & b &= y_1-y_2 & c &= r_1 \pm r_2 \end{aligned} $$
$$\begin{aligned} S_t = \frac{b \sqrt{a^2+b^2-c^2} \pm ac}{a \sqrt{a^2+b^2-c^2} \mp bc} \end{aligned}$$
$$\begin{aligned} x_i &= x_1 \mp \frac{S_t r_1}{\sqrt{S_t^2+1}} & y_i &= \pm \sqrt{r_1^2-(x_i-x_1)^2}+y_1 \end{aligned}$$
$$\begin{aligned} y &= S_t(x - x_i) + y_i \end{aligned}$$
Substitute $(x_1, y_1)$ with the coordinates of the first circle and $r_1$ with its radius. Likewise, substitute $x_2$, $y_2$, and $r_2$ for the second circle.
Use different states of the three plus–minus signs to generate eight different possible lines, and manually choose four from those eight as your four tangent lines (two internal and two external).
introduction
A couple years ago, i sometimes liked to make art in Desmos (an online graphing calculator), and one of my almost-finished pieces was a bicycle. I had written the equation for each line that made up the drawing of the bike, and i could even adjust the seat height and pedal lengths with variable sliders.
However, one feature of the bike was notably missing: the chain connecting the gears. This would have taken the form of lines tangent to the two circles representing the gears, but i didn’t know how to graph that precisely at the time.

I’ve since lost the original Desmos project, but my unsolved problem has tormented me ever since. How do you write the linear equation for each of the lines that are tangent to two circles if you know the radii and coordinates of those circles?
external tangent lines
There are two circles:
- Circle 1 with center $C_1=(x_1,y_1)$ and radius $r_1$
- Circle 2 with center $C_2=(x_2,y_2)$ and radius $r_2$
- $r_1\geq r_2$
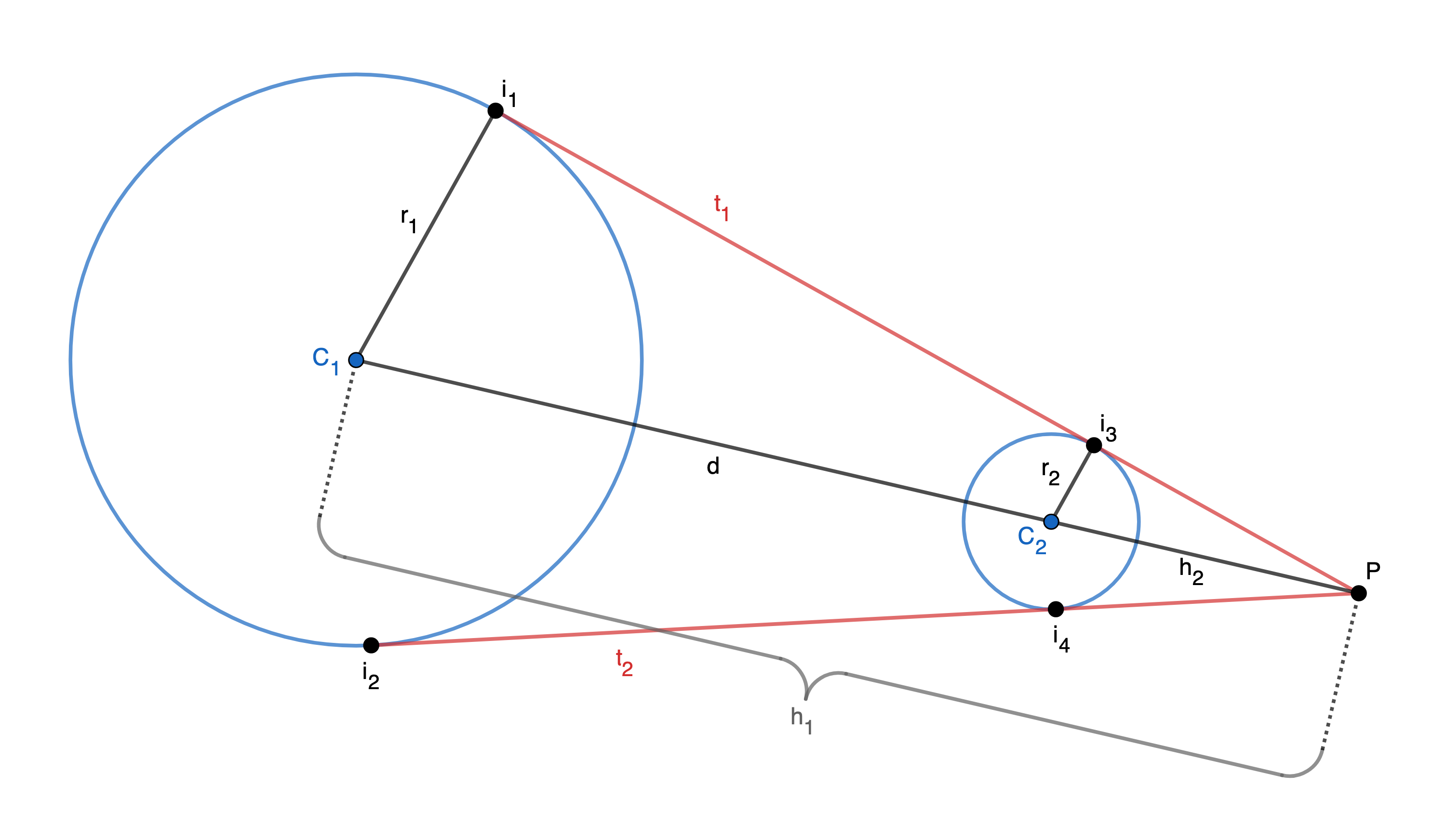
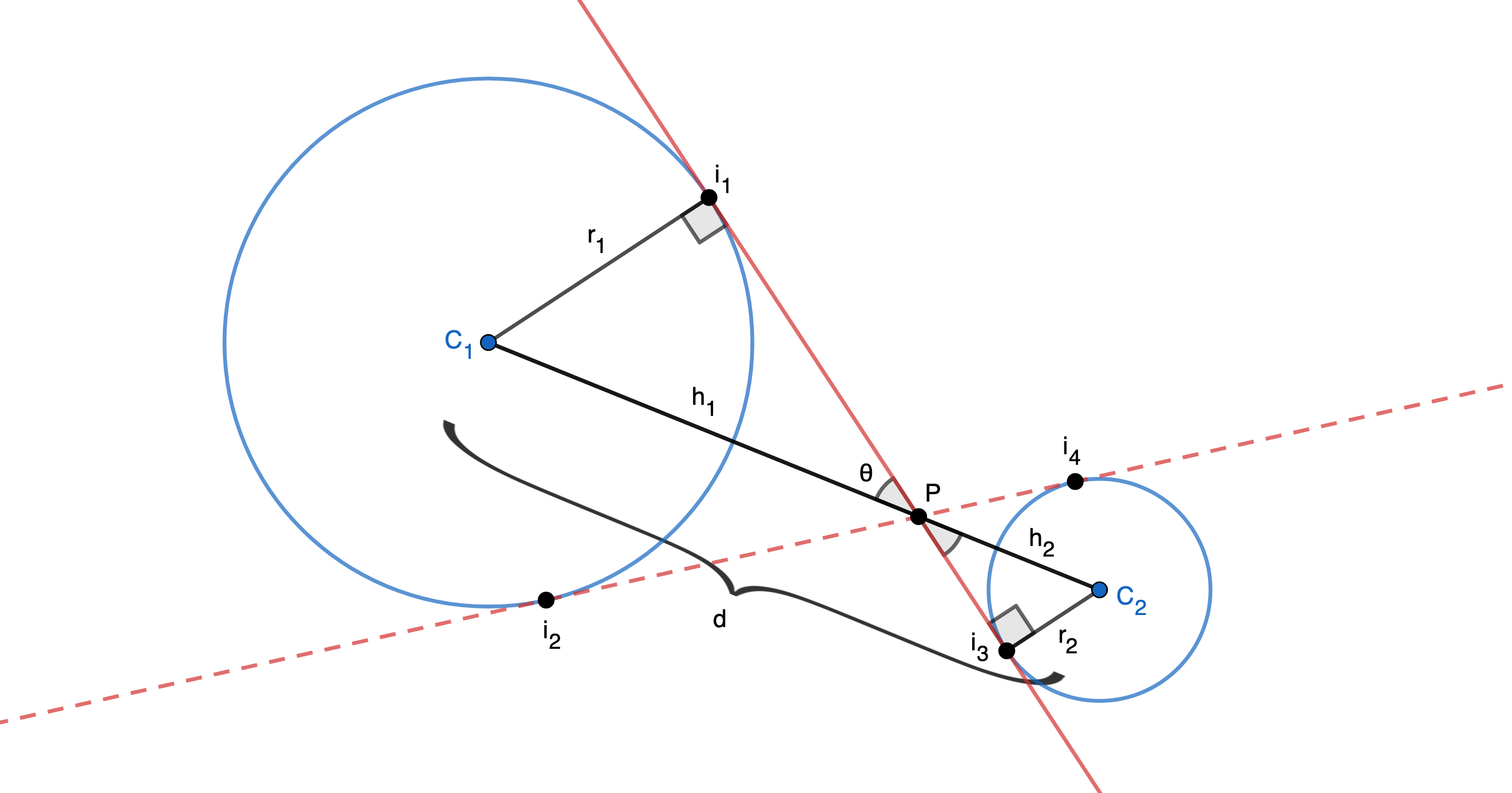
A line is drawn between the centers of the circles, called $C(x)$, and both external tangent lines $t_1(x)$ and $t_2(x)$ are drawn. The points of intersection between the tangent lines and circle 1 are $i_1=(x_{i1},y_{i1})$ and $i_2=(x_{i2},y_{i2})$. The points of intersection on circle 2 are $i_3=(x_{i3},y_{i3})$ and $i_4=(x_{i4},y_{i4})$. All three lines intersect at point $P$. The angle between the first tangent line and the line that connects the centers of the circles is $\angle C_1Pi_1$.
slopes of the external tangents
Angle $\angle C_1 i_1 P$ is a right angle because it is the angle between a tangent to a circle and a radius that passes through the point of tangency, and the same is true for $\angle C_2 i_3 P$. Because these right angles are congruent, and because $\triangle C_1 P i_1$ and $\triangle C_2 P i_2$ share the angle $\angle C_1 P i_1$, this makes the triangles similar.
Because these triangles are similar, the ratio between corresponding sides is constant. Therefore,
$$\frac{r_1}{r_2} = \frac{h_1}{h_2}$$
We can substitute $h_1$ with the two lengths that make it up: $h_2+d$. Then, by rewriting the equation, we can solve for $h_2$.
$$ \begin{aligned} \frac{r_1}{r_2} &= \frac{h_2+d}{h_2} \\ r_1h_2 &= r_2(h_2+d) \\ r_1h_2 &= r_2h_2+r_2d \\ r_1h_2 &= r_2h_2+r_2d \\ r_1h_2-r_2h_2 &= r_2d \\ h_2(r_1-r_2) &= r_2d \\ h_2 &= \frac{r_2d}{r_1-r_2} \end{aligned} $$
Now that $h_2$ is defined, we can use trigonometry to define the angle between the line that connects the circles’ centers and the first tangent line. This angle is $\angle C_2 P i_3$, or $\theta$.
Consider triangle $\triangle C_2 i_3 P$:
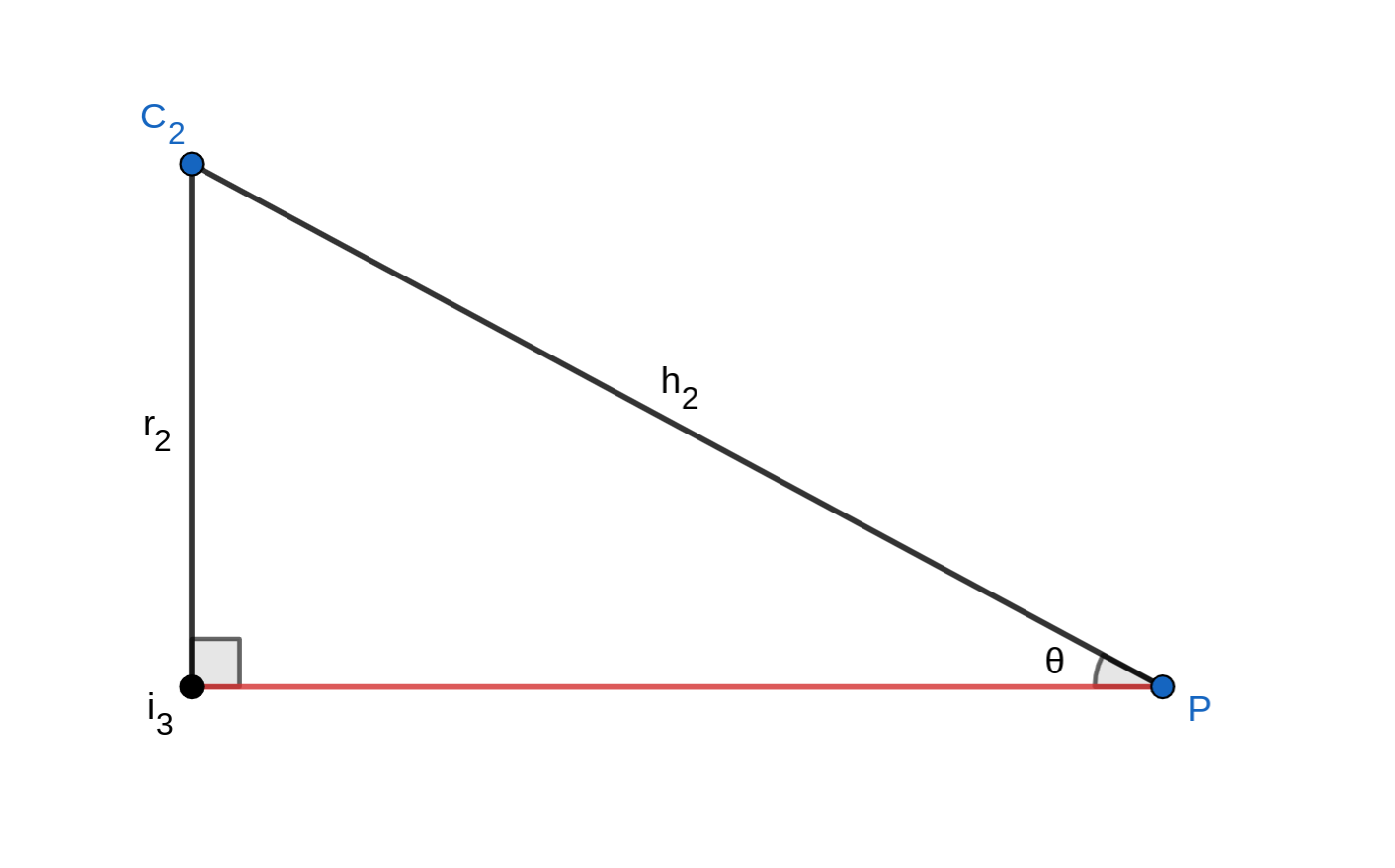
Because of the definition of the sine of an angle (the ratio between the opposing side and the hypotenuse in a right triangle), $\sin{\theta} =\frac{r_2}{h_2}$. By taking the inverse sine of each side, we can define $\theta$: $$\theta =\arcsin{\left(\frac{r_2}{h_2}\right)}$$ To find the angle of the first external tangent line, we can add $\theta$ to the angle of $C(x)$ with respect to the $x$-axis. Similarly, we can subtract $\theta$ from the angle of $C(x)$ to find the angle of the second tangent line. $$\begin{aligned} \theta_t=\theta_C \pm \theta \end{aligned}$$
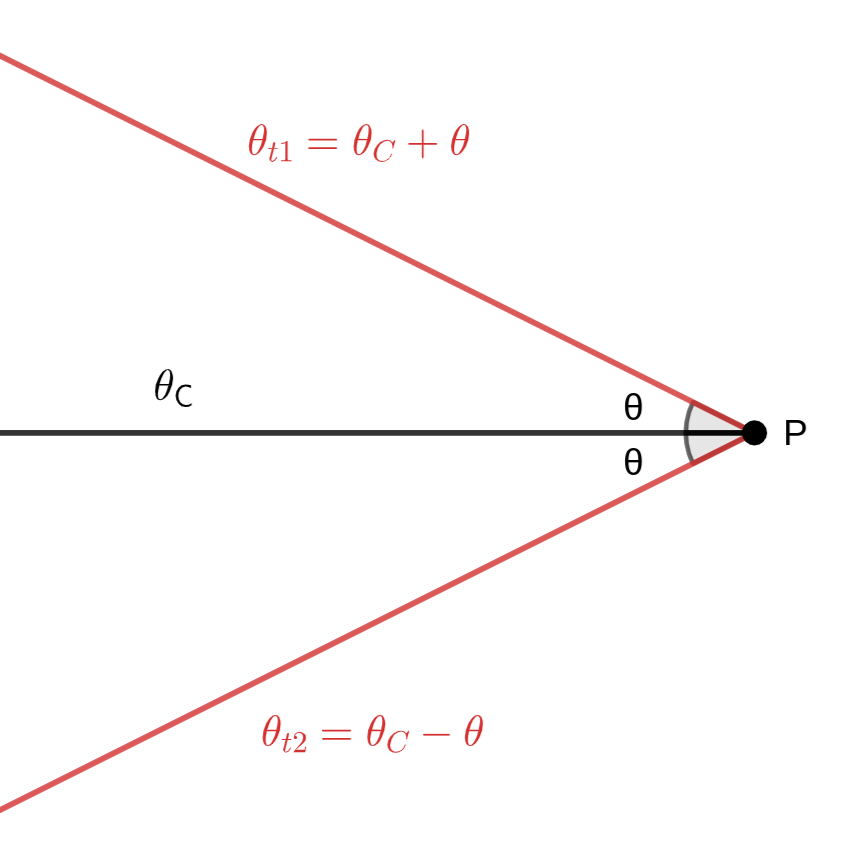
But how do we know the angle of $C(x)$? The slope of $C(x)$ can be found by using the slope formula and substituting with the coordinates of the centers of the circles. Then, we can convert this slope into an angle by finding its inverse tangent.
$$\begin{aligned} \theta_C &= \arctan{\left( S_C \right)} \\ \theta_C &= \arctan{\left( \frac{\Delta y}{\Delta x} \right)} \\ \theta_C &= \arctan{\left( \frac{y_1-y_2}{x_1-x_2} \right)} \end{aligned} $$
Now, we can substitute the values of $\theta_C$ and $\theta$: $$ \begin{aligned} \theta_t &= \theta_C \pm \theta \\ \theta_C &= \arctan{\left( \frac{y_1-y_2}{x_1-x_2} \right)} \\ \theta &= \arcsin{\left( \frac{r_2}{h_2} \right)} \\ \theta_t &= \arctan{\left( \frac{y_1-y_2}{x_1-x_2} \right)} \pm \arcsin{\left( \frac{r_2}{h_2} \right)} \end{aligned} $$
Then, we can substitute for $h_2$ and simplify:
$$ \begin{aligned} h_2 &= \frac{r_2d}{r_1-r_2} \\ \theta_t &= \arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \pm \arcsin{\left(\frac{r_2}{\frac{r_2d}{r_1 - r_2}}\right)} \\ \theta_t &= \arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \pm \arcsin{\left(\frac{r_2(r_1 - r_2)}{r_2d}\right)} \\ \theta_t &= \arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \pm \arcsin{\left(\frac{r_1 - r_2}{d}\right)} \end{aligned} $$
We can then substitute for $d$. $d$ is the distance between the centers of the circles, so we can use the distance formula with $C_1$ and $C_2$ as points.
$$ \begin{aligned} d &= \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \\ \theta_t &= \arctan{\left( \frac{y_1-y_2}{x_1-x_2} \right)} \pm \arcsin{\left(\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)} \end{aligned} $$
Because the tangent of the angle of a line produces its slope, we can take the tangent of both sides to generate an equation for both of the slopes of the external tangent lines: $$S_t = \tan{\left(\arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \pm \arcsin{\left(\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)}\right)}$$ This equation, which uses trigonometric functions inside of a trigonometric function, is not very elegant. To rewrite it, we can use a trigonometric identity for the tangent of a sum or difference:
$$\tan{(\alpha \pm \beta)}=\frac{\tan{(\alpha)} \pm \tan{(\beta)}}{1 \mp \tan{(\alpha)}\tan{(\beta)}}$$
In this case, $\alpha = \arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)}$ and $\beta = \arcsin{\left(\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)}$.
For ease of explanation, we’ll first find $\tan{(\alpha)}$ and $\tan{(\beta)}$ separately, then substitute them into the identity.
The tangent of $\alpha$ is simple to find, because the arctangent and the tangent functions cancel each other out:
$$\begin{aligned} \tan{(\alpha)} &= \tan{\left( \arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \right)} \\ \tan{(\alpha)} &= \frac{y_1-y_2}{x_1-x_2} \end{aligned}$$
However, the tangent of $\beta$ is trickier because the tangent function doesn’t cancel out the arcsine function. To remedy this, we can use an identity for the tangent of an arcsine, as demonstrated by figure 5.
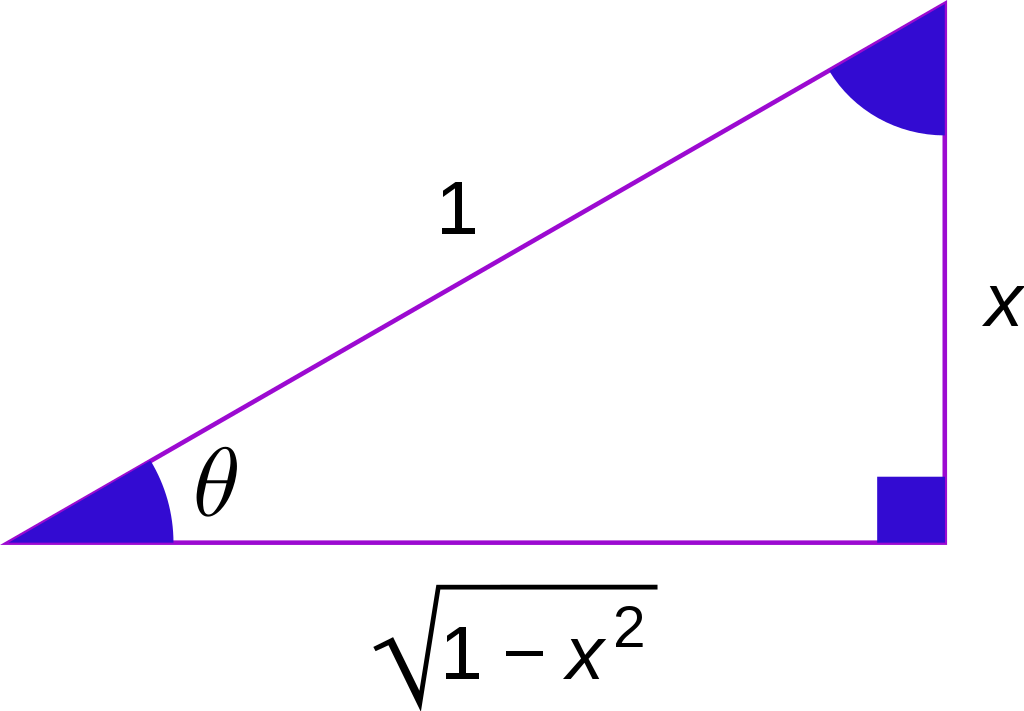
In figure 5, the sine of angle $\theta$ is the ratio between the lengths of the opposite side and the hypotenuse, or $\frac{x}{1}=x$. Therefore, the arcsine of this ratio equals $\theta$: $$\arcsin{(x)}=\theta$$ The tangent of $\theta$, or in other words, the tangent of $\arcsin{(x)}$, is equal to the ratio between the opposite side and the adjacent side. The length of the adjacent side can be found using the Pythagorean theorem: $\sqrt{1-x^2}$. Therefore, $$\tan{\left(\arcsin{(x)}\right)}=\frac{x}{\sqrt{1-x^2}}$$ We can now use this identity to find $\tan{(\beta)}$: $$ \begin{aligned} \tan{(\beta)} &= \tan{\left(\arcsin{\left(\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)}\right)} \\ \tan{(\beta)} &= \frac{\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}}{\sqrt{1-\left(\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)^2}} \\ \tan{(\beta)} &= \frac{\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}}{\sqrt{1-\frac{(r_1 - r_2)^2}{(x_1-x_2)^2+(y_1-y_2)^2}}} \\ \tan{(\beta)} &= \frac{\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}}{\sqrt{\frac{(x_1-x_2)^2+(y_1-y_2)^2}{(x_1-x_2)^2+(y_1-y_2)^2}-\frac{(r_1 - r_2)^2}{(x_1-x_2)^2+(y_1-y_2)^2}}} \\ \tan{(\beta)} &= \frac{\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}}{\sqrt{\frac{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}{(x_1-x_2)^2+(y_1-y_2)^2}}} \\ \tan{(\beta)} &= \frac{\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}}{\frac{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}} \\ \tan{(\beta)} &= \frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}} \end{aligned} $$ Now that we know $\tan{(\alpha)}$ and $\tan{(\beta)}$, we can return to rewriting the slope equation using the identity for the tangent of a sum or difference.
$$ \begin{aligned} S_t &= \tan{\left(\arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \pm \arcsin{\left(\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)}\right)} \\ \tan{(\alpha \pm \beta)} &= \frac{\tan{(\alpha)} \pm \tan{(\beta)}}{1 \mp \tan{(\alpha)}\tan{(\beta)}} \\ S_t &= \frac{\frac{y_1-y_2}{x_1-x_2} \pm \frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}}{1 \mp \frac{y_1-y_2}{x_1-x_2} \cdot \frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}} \\ S_t &= \frac{\frac{y_1-y_2}{x_1-x_2} \pm \frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}}{1 \mp \frac{(y_1-y_2)(r_1 - r_2)}{(x_1-x_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}} \end{aligned} $$
We can rewrite each term with a common denominator. $$\begin{aligned} S_t &= \frac{\frac{(y_1-y_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}{(x_1-x_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}} \pm \frac{(x_1-x_2)(r_1 - r_2)}{(x_1-x_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}}{\frac{(x_1-x_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}{(x_1-x_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}} \mp \frac{(y_1-y_2)(r_1 - r_2)}{(x_1-x_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2}}} \end{aligned}$$ Finally, multiplying each side by the common denominator yields the final equation for the slopes of the external tangent lines: $$S_t = \frac{(y_1-y_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2} \pm (x_1-x_2)(r_1 - r_2)}{(x_1-x_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2} \mp (y_1-y_2)(r_1 - r_2)}$$ At first glance, this equation doesn’t appear any simpler than the one involving nested trigonometric functions. However, by applying the following substitutions, the symmetry and elegance of this equation becomes clear: $$\begin{gathered} a = x_1-x_2 \qquad b = y_1-y_2 \qquad c = r_1-r_2 \\ S_t = \frac{b \sqrt{a^2+b^2-c^2} \pm ac}{a \sqrt{a^2+b^2-c^2} \mp bc} \end{gathered}$$
points on the external tangents
In order to define an exact equation for the external tangents, defining the slopes isn’t enough. We also need a point on each of the slopes, and the easiest points to use are the points of tangency on circle 1.
A point of tangency on circle 1 will have an instantaneous slope equal to that of the tangent line it corresponds to. Therefore, to figure out which points on circle 1 can qualify as points of tangency, we need to find the derivative (the slope at each point) of the equation of circle 1 and set it equal to the tangent’s slope, and then solve for the x-value of the point of tangency. This can then be fed back into the circle equation to define the other coordinate of the point of tangency, which would complete the definition of the tangent line function.
This method presents one key problem, however: a circle equation is not a function, and so its derivative would not be a function either. At each x-value in the domain of the graph of the circle, there are two possible y-values and two possible slopes, and as a result, there are two points on circle 1 that could qualify as points of tangency for each tangent line. Because there are two tangent lines, this makes four possible points of tangency, but only two of them are correct.
Ultimately, i decided to accept the fact that this approach would generate not two, but four possible external tangents, and someone using this equation would have to manually decide which definitions to use.
The first step is to find the derivative of the circle equation. However, this equation is not defined simply in terms of $y$, as it’s based on the Pythagorean theorem. $$(x-x_1)^2+(y-y_1)^2=r_1^2$$ Implicit differentiation would not work in this case, so we need to rewrite the circle equation in terms of $y$ before we differentiate it with respect to $x$. $$\begin{aligned} (x-x_1)^2+(y-y_1)^2 &= r_1^2 \\ (y-y_1)^2 &= r_1^2-(x-x_1)^2 \\ y-y_1 &= \pm \sqrt{r_1^2-(x-x_1)^2} \\ y &= \pm \sqrt{r_1^2-(x-x_1)^2}+y_1 \end{aligned}$$ Now, we can find the derivative of this equation to find the slope of any given point on circle 1.
$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x} [y] &= \frac{\mathrm{d}}{\mathrm{d}x} \left[ \pm \sqrt{r_1^2-(x-x_1)^2}+y_1 \right] \\ \frac{\mathrm{d}y}{\mathrm{d}x} &= \pm \frac{\mathrm{d}}{\mathrm{d}x} \left[ \sqrt{r_1^2-(x-x_1)^2} \right] \\ \frac{\mathrm{d}y}{\mathrm{d}x} &= \pm \frac{\mathrm{d}}{\mathrm{d}x} \left[ \left( r_1^2-(x-x_1)^2 \right)^{\frac{1}{2}} \right] \end{aligned}$$
We can use the chain rule for derivatives to continue. $$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}x} &= \pm \frac{1}{2} \left( r_1^2-(x-x_1)^2 \right)^{-\frac{1}{2}} \left( \frac{\mathrm{d}}{\mathrm{d}x} \left[ r_1^2-(x-x_1)^2 \right] \right) \\ \frac{\mathrm{d}y}{\mathrm{d}x} &= \pm \frac{1}{2 \sqrt{r_1^2-(x-x_1)^2}} \left( -\frac{\mathrm{d}}{\mathrm{d}x} \left[ (x-x_1)^2 \right] \right) \\ \frac{\mathrm{d}y}{\mathrm{d}x} &= \pm \frac{1}{2 \sqrt{r_1^2-(x-x_1)^2}} \left( 2(x-x_1)(1) \right) \\ \frac{\mathrm{d}y}{\mathrm{d}x} &= \pm \frac{2(x-x_1)}{2 \sqrt{r_1^2-(x-x_1)^2}} \\ \frac{\mathrm{d}y}{\mathrm{d}x} &= \pm \frac{x-x_1}{\sqrt{r_1^2-(x-x_1)^2}} \end{aligned}$$ This resulting equation gives the relationship between the slope of the tangent line ($\frac{\mathrm{d}y}{\mathrm{d}x}$) and the $x$-coordinate of the point of tangency on circle 1.
We need to rewrite this equation in terms of $x$, because in this case, $x$ is the $x$-coordinate of the point of tangency, which will be used in the tangent line equation. However, the algebra that enables us to do this is long and confusing. To help make the process easier to read, we will temporarily reassign each variable to a single letter each: $$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}x} = S_t &= a \\ r_1 &= b \\ x = x_i &= c \\ x_1 &= d \end{aligned}$$ Essentially, we can rewrite the equation as a sum of terms, which can be rearranged into a quadratic equation with multi-term coefficients. These can be plugged into the quadratic formula in order to solve for $c$, which represents $x_i$. $$\begin{aligned} a &= \pm \frac{c-d}{\sqrt{b^2-(c-d)^2}} \\ \pm a \sqrt{b^2-(c-d)^2} &= c-d \\ \left( \pm a \sqrt{b^2-(c-d)^2} \right)^2 &= (c-d)^2 \\ a^2(b^2-(c-d)^2) &= (c-d)^2 \\ a^2(b^2-(c^2-2cd+d^2)) &= c^2 - 2cd +d^2 \\ a^2(b^2-c^2+2cd-d^2) &= c^2 - 2cd +d^2 \\ a^2b^2-a^2c^2+2a^2cd-a^2d^2 &= c^2 - 2cd +d^2 \\ a^2b^2 - a^2c^2 + 2a^2cd - a^2d^2 - c^2 + 2cd - d^2 &= 0 \\ - a^2c^2 - c^2 + 2a^2cd + 2cd + a^2b^2 - a^2d^2 - d^2 &= 0 \\ c^2(- a^2 - 1) + c(2a^2d + 2d) + (a^2b^2 - a^2d^2 - d^2) &= 0 \end{aligned}$$ Now that the equation is in the form of a quadratic, we can use the quadratic formula to determine the solutions for $c$. $$c = \frac{-(2a^2d+2d) \pm \sqrt{(2a^2d+2d)^2-4(-a^2-1)(a^2b^2 - a^2d^2 - d^2)}}{2(-a^2-1)}$$ For readability, we’ll simplify the radicand in the quadratic formula separately: $$\begin{gathered} (2a^2d+2d)^2-4(-a^2-1)(a^2b^2 - a^2d^2 - d^2) \\ 4a^4d^2 + 8a^2d^2 + 4d^2 - 4(-a^4b^2 + a^4d^2 +a^2d^2 -a^2b^2 +a^2d^2 +d^2) \\ 4a^4d^2 + 8a^2d^2 + 4d^2 + 4a^4b^2 - 4a^4d^2 - 4a^2d^2 + 4a^2b^2 - 4a^2d^2 - 4d^2 \\ (4a^4d^2 - 4a^4d^2) + (8a^2d^2 - 4a^2d^2 - 4a^2d^2) + (4d^2 - 4d^2) + 4a^4b^2 + 4a^2b^2 \\ 4a^4b^2 + 4a^2b^2 \end{gathered}$$ Then, we can substitute the radicand back into the quadratic formula and continue simplifying. $$\begin{aligned} c &= \frac{-(2a^2d+2d) \pm \sqrt{4a^4b^2 + 4a^2b^2}}{2(-a^2-1)} \\ c &= \frac{-2d(a^2+1) \pm \sqrt{4a^4b^2 + 4a^2b^2}}{-2(a^2+1)} \\ c &= \frac{-2d(a^2+1) \pm 2ab\sqrt{a^2+1}}{-2(a^2+1)} \\ c &= \frac{d(a^2+1) \mp ab \sqrt{a^2+1}}{a^2+1} \\ c &= \frac{d(a^2+1)}{a^2+1} \mp \frac{ab \sqrt{a^2+1}}{a^2+1} \\ c &= d \mp \frac{ab \sqrt{a^2+1}}{a^2+1} \\ c &= d \mp \frac{ab (a^2+1)^{\frac{1}{2}}}{(a^2+1)^1} \\ c &= d \mp ab(a^2+1)^{-\frac{1}{2}} \\ c &= d \mp ab \cdot \frac{1}{(a^2+1)^{\frac{1}{2}}} \\ c &= d \mp \frac{ab}{\sqrt{a^2+1}} \end{aligned}$$ We can now reverse the temporary substitutions to give us a definition of the $x$-coordinate of the point of tangency on circle 1. $$\begin{gathered} a = S_t \qquad b = r_1 \qquad c = x_i \qquad d = x_1 \\ x_i = x_1 \mp \frac{S_t r_1}{\sqrt{S_t^2+1}} \end{gathered}$$ This equation is in terms of the slope of the tangent line, the $x$-coordinate of the center of circle 1, and the radius of circle 1. However, it’s important to note that the tangent’s slope is itself defined by other given values in the problem. Earlier, we manipulated the circle equation so that it was in terms of $y$, which allowed us to find its derivative with respect to $x$. We can substitute our definition of the $x$-coordinate of the point of tangency into this circle equation, allowing us to define the corresponding $y$-coordinate. $$y_i = \pm \sqrt{r_1^2-(x_i-x_1)^2}+y_1$$
final external tangent model
The slopes of the tangent lines, the $x$-coordinates of the points of tangency, and the $y$-coordinates of the points of tangency have all been defined in terms of the original parameters of the problem. By using the point-slope equation $f(x) = m (x - x_1) + y_1$, the final system of equations can be displayed: $$\begin{aligned} S_t &= \frac{(y_1-y_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2} \pm (x_1-x_2)(r_1 - r_2)}{(x_1-x_2)\sqrt{(x_1-x_2)^2+(y_1-y_2)^2-(r_1 - r_2)^2} \mp (y_1-y_2)(r_1 - r_2)} \\ x_i &= x_1 \mp \frac{S_t r_1}{\sqrt{S_t^2+1}} \\ y_i &= \pm \sqrt{r_1^2-(x_i-x_1)^2}+y_1 \\ y &= S_t(x - x_i) + y_i \end{aligned}$$ Unfortunately, because of the ambiguity of the plus-or-minus operators in the system of equations, two of the possible equations generated are not correct, and so the correct equations must be chosen manually.
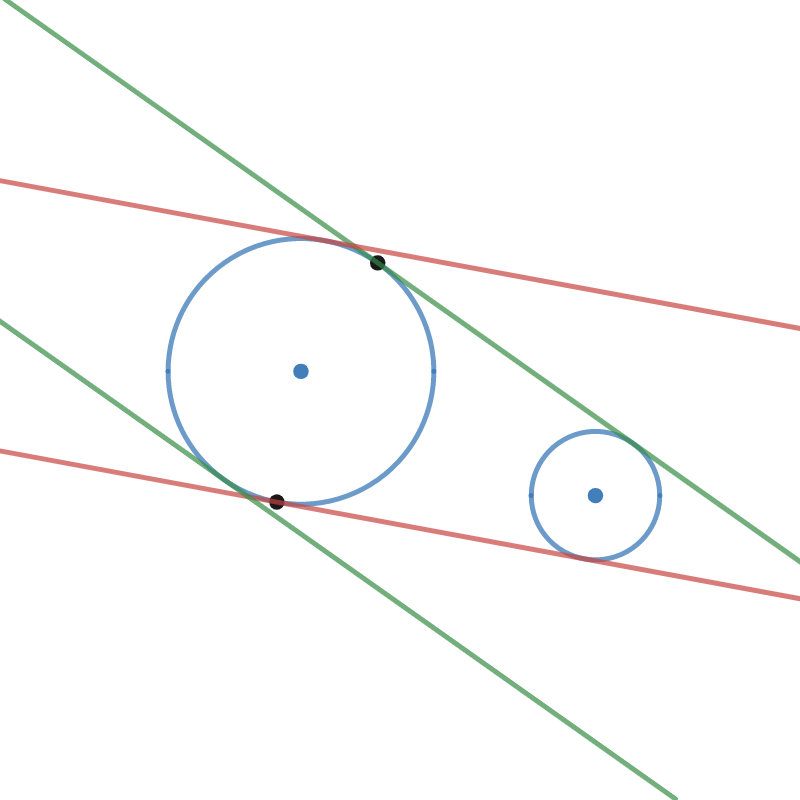
internal tangent lines
The process for modelling the internal tangents to two circles is very similar to the process for external tangents. In figure 2, two similar triangles were used to write a ratio involving the radii and the hypotenuses. In figure 8, triangles $\triangle C_1 P i_1$ and $\triangle C_2 P i_3$ are similar because they share the vertical angle $\theta$, and they both have a right angle. This allows us to equate the following ratios between corresponding sides: $$\frac{r_2}{r_1}=\frac{h_2}{h_1}$$ We can rewrite $h_2$ as $d-h_1$ and then solve for $h_1$: $$\begin{aligned} \frac{r_2}{r_1} &= \frac{d-h_1}{h_1} \\ \frac{h_1r_2}{r_1} &= d-h_1\\ h_1r_2 &= r_1d-r_1h_1\\ h_1r_2 +r_1h_1&= r_1d\\ h_1(r_2 +r_1) &= r_1d\\ h_1 &= \frac{r_1d}{r_2 +r_1} \end{aligned}$$ This definition of $h_1$ allows us to find $\theta$ using trigonometry. We can express the sine of $\theta$ as the ratio between the opposite side in the right triangle and the hypotenuse: $$\sin{(\theta)=\frac{r_1}{h_1}}$$ Then, we can substitute for $h_1$ and solve for $\theta$. $$\begin{aligned} \sin{(\theta)}&=\frac{r_1}{ \frac{r_1d}{r_2 +r_1}} \\ \sin{(\theta)}&=\frac{r_1(r_2 +r_1)}{r_1d} \\ \sin{(\theta)}&=\frac{r_2 +r_1}{d} \\ \theta&=\arcsin{\left(\frac{r_2 +r_1}{d}\right)} \end{aligned}$$ Just like the external tangents, the angle of the internal tangents is simply the angle of $C(x)$, plus or minus the angle $\theta$ (see figure 4{reference-type=“ref” reference=“fig:plusMinusTheta”}). Because we already found the angle of $C(x)$ (called $\theta_C$) when we modeled the external tangents, we can use a similar formula as before: $$\begin{aligned} \theta_t &= \theta_C \pm \theta \\ \theta_C &= \arctan{\left( \frac{y_1-y_2}{x_1-x_2} \right)} \\ \theta_t &= \arctan{\left( \frac{y_1-y_2}{x_1-x_2} \right)} \pm \arcsin{\left(\frac{r_2 +r_1}{d}\right)} \end{aligned}$$ Then, because the tangent of the angle of a line equals the slope of the line, we can take the tangent of each side to find the slope of the internal tangent lines. $$S_t = \tan{\left(\arctan{\left( \frac{y_1-y_2}{x_1-x_2} \right)} \pm \arcsin{\left(\frac{r_2 +r_1}{d}\right)}\right)}$$ Finally, we can substitute $d$ with the formula for the distance between $C_1$ and $C_2$. $$S_t = \tan{\left(\arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \pm \arcsin{\left(\frac{r_1 + r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)}\right)}$$ This is very similar to the formula for the slope of the external tangent lines. In fact, the sole difference between the formulas is that the external tangent equation uses the difference between the circles' radii, while the internal tangent equation uses the sum of the radii. $$\begin{aligned} S_{\text{outer tangents}} &= \tan{\left(\arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \pm \arcsin{\left(\frac{r_1 - r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)}\right)} \\ S_{\text{inner tangents}} &= \tan{\left(\arctan{\left(\frac{y_1-y_2}{x_1-x_2}\right)} \pm \arcsin{\left(\frac{r_1 + r_2}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right)}\right)} \end{aligned}$$ Conveniently, this difference is consistent throughout the rest of the problem. At no point during the problem-solving process involving the external tangents was the term $r_1-r_2$ separated or modified, which means that all we need to do to adapt our model to use for the internal tangents is to replace $r_1-r_2$ with $r_1+r_2$. Or, to represent both set of tangents in the same system of equations, we can use $r_1 \pm r_2$.
final model
If we rearrange the previous system of equations for external tangent lines, as well as replace $r_1-r_2$ with $r_1 \pm r_2$, the updated system of equations can be displayed. We can mathematically model tangent lines to two circles on the coordinate plane using the following system of equations:
$$ \begin{aligned} a &= x_1-x_2 & b &= y_1-y_2 & c &= r_1 \pm r_2 \end{aligned} $$
$$\begin{aligned} S_t = \frac{b \sqrt{a^2+b^2-c^2} \pm ac}{a \sqrt{a^2+b^2-c^2} \mp bc} \end{aligned}$$
$$\begin{aligned} x_i &= x_1 \mp \frac{S_t r_1}{\sqrt{S_t^2+1}} & y_i &= \pm \sqrt{r_1^2-(x_i-x_1)^2}+y_1 \end{aligned}$$
$$\begin{aligned} y &= S_t(x - x_i) + y_i \end{aligned}$$
Note that in each of the first three lines in the system of equations, there are one or more uses of the plus-or-minus or minus-or-plus operator. This means that there are $2^3=8$ possible linear functions that this system could generate, depending on which option (plus or minus) one chooses for each line in the system. Only four of these functions, however, will represent actual tangents, internal or external, to the circles.
limitations of the model
As previously noted, the biggest limitation in this model is that it’s ambiguous: only half of the lines it produces are real tangent lines, so someone using the model would need to manually choose which set to use. There are some situations in which the model breaks – for example, when one or more of the tangent lines would be vertical, the model produces an undefined slope.